TL;DR:
This weblog introduces retrospective simulation, impressed by Taleb’s “Fooled by Randomness,” to simulate 1,000 alternate historic value paths utilizing a non-parametric Brownian bridge technique. Utilizing SENSEX knowledge (2000–2020) as in-sample knowledge, the writer optimises an EMA crossover technique throughout the in-sample knowledge first, after which applies it to the out-of-sample knowledge utilizing the optimum parameters obtained from the in-sample backtest. Whereas the technique outperforms the buy-and-hold method in in-sample testing, it considerably underperforms in out-of-sample testing (2020–2025), highlighting the chance of overfitting to a single realised path. The writer then runs the backtest throughout all simulated paths to determine essentially the most often profitable SEMA-LEMA parameter mixtures.
The writer additionally calculates VaR and CVaR utilizing over 5 million simulated returns and compares return extremes and distributional traits, revealing heavy tails and excessive kurtosis. This framework allows extra strong technique validation by evaluating how methods would possibly carry out throughout a number of believable market eventualities.
Introduction
In “Fooled by Randomness”, Taleb says at one place, “To start with, once I knew near nothing (that’s, even lower than at present), I questioned whether or not the time sequence reflecting the exercise of individuals now lifeless or retired ought to matter for predicting the long run.”
This bought me pondering. We frequently run simulations for the possible paths a time sequence can take sooner or later. Nonetheless, the premise for these simulations is predicated on historic knowledge. Given the stochastic nature of asset costs (learn extra), the realised value path had the selection of an infinite variety of paths it may have taken, nevertheless it traversed by solely a type of infinite prospects. And I believed to myself, why not simulate these alternate paths?
In widespread follow, this method is known as bootstrap historic simulation. I selected to discuss with it as retrospective simulation, as a extra intuitive counterpart to the phrases ‘look-ahead’ and ‘walk-forward’ used within the context of simulating the long run.
Article map
Right here’s a top level view of how this text is laid out:
Knowledge Obtain
We import the required libraries and obtain the day by day knowledge of the SENSEX index, a broad market index based mostly on the Bombay Inventory Alternate of India.
I’ve downloaded the info from January 2000 to November 2020 because the in-sample knowledge, and from December 2020 to April 2025 because the out-of-sample knowledge. We may have put in a spot (an embargo) between the in-sample and out-of-sample knowledge to minimise, if not eradicate, knowledge leakage (learn extra). In our case, there’s no direct knowledge leakage. Nonetheless, since inventory ranges (costs) are identified to bear autocorrelation, like we noticed above, the SENSEX index on the primary buying and selling day of December 2020 can be extremely correlated with its degree on the final buying and selling day of November 2020.
Thus, after we prepare our mannequin on knowledge that features the final buying and selling day of November 2020, it extracts info from that day’s degree and makes use of it to get skilled. Since our testing dataset is from the primary buying and selling day of December 2020, some residual info from the coaching dataset is current within the testing dataset.
As an extension, the coaching set accommodates some info that can also be current within the testing dataset. Nonetheless, this info will diminish over time and finally grow to be insignificant. Having mentioned that, I didn’t keep a spot between the in-sample and out-of-sample datasets in order that we are able to concentrate on understanding the core idea of this text.
You should utilize any yfinance ticker to obtain knowledge for an asset of your liking. It’s also possible to regulate the dates to fit your wants.
Retrospective Simulation utilizing Brownian Bridge
The subsequent half is the primary crux of this weblog. That is the place I simulate the doable paths the asset may have taken from January 2000 to November 2020. I’ve simulated 1000 paths. You possibly can modify it to make it 100 or 10000, as you want. The upper the worth, the larger our confidence within the outcomes, however there’s a tradeoff in computational time. I’ve simulated solely the closing costs. I stored the first-day and last-day costs the identical because the realised ones, and simulated the in-between costs.
Preserving the worth fastened on the primary day is smart. However the final day? If the costs are to observe a random stroll (learn extra), the closing value ranges of most, if not all, paths must be totally different, isn’t it? However I made an assumption right here. Given the environment friendly market speculation, the index would have a good value by the top of November 2020, and after transferring on its capricious course, it might converge again to this honest value.
Why solely November 2020?
Was the extent of the index at its fairest value at the moment? No manner of realizing. Nonetheless, one date is pretty much as good as some other, and we have to work with a particular date, so I selected this one.
One other consideration right here is on what foundation we permit the simulated paths to meander. Ought to it’s parametric, the place we assume the time sequence to observe a particular distribution, or non-parametric, the place we don’t make any such assumption? I selected the latter. The monetary literature discusses costs (and their returns) as belonging roughly to sure underlying distributions. Nonetheless, in terms of outlier occasions, equivalent to extremely risky value jumps, these assumptions start to interrupt down, and it’s these occasions {that a} quant (dealer, portfolio supervisor, investor, analyst, or researcher) must be ready for.
For the non-parametric method, I’ve modified the Brownian bridge method. In a pure Brownian bridge method, the returns are assumed to observe a Gaussian distribution, which once more turns into considerably parametric (learn extra). Nonetheless, in our method, we calculate the realized returns from the in-sample closing costs and use these returns as a pattern for the simulation generator to select from. We’re utilizing bootstrapping with substitute (learn extra), which signifies that the realized returns aren’t simply being shuffled; some values could also be repeated, whereas some will not be used in any respect. If the values are merely shuffled, all simulated paths would land on the final closing value of the in-sample knowledge. How can we make sure that the simulated costs converge to the ultimate shut value of the in-sample knowledge? We’ll use geometric smoothing for that.
One other consideration: since we use the realized returns, we’re priming the simulated paths to resemble the realized path, right? Kind of, but when we have been to generate pseudo-random numbers for these returns, we must make some assumption about their distribution, making the simulation a parametric course of.
Right here’s the code for the simulations:
Notice that I didn’t use a random seed when producing the simulated paths. I’ll point out the rationale at a later stage.
Let’s plot the simulated paths:
The above graph exhibits that the beginning and ending costs are the identical for all 1,000 simulated paths. We must always notice one factor right here. Since we’re working with knowledge from a broad market index, whose ranges rely on many interlinked macroeconomic variables and components, it is extremely unlikely that the index would have traversed a lot of the paths simulated above, given the identical macroeconomic occasions that occurred in the course of the simulation interval. We’re making an implicit assumption right here that the desired macroeconomic variables and components differ in every of the simulated paths, and the interactions between these variables and components consequence within the simulated ranges that we generate. This holds for some other asset class or asset you resolve to switch the SENSEX index with, for retrospective simulation functions.
Exponential Transferring Common Crossover Technique Growth and Backtesting on In-Pattern Knowledge, and Parameter Optimisation
Subsequent, we develop a easy buying and selling technique and conduct a backtest utilizing the in-sample knowledge. The technique is a straightforward exponential transferring common crossover technique, the place we go lengthy when the short-period exponential transferring common (SEMA) of the shut value goes above the long-period exponential transferring common (LEMA), and we go quick when the SEMA crosses the LEMA from above (learn extra).
Via optimisation, we’ll try to seek out the perfect SEMA and LEMA mixture that yields the utmost returns. For the SEMA, I exploit lookback intervals of 5, 10, 15, 20, … as much as 100, and for the LEMA, 20, 30, 40, 50, … as much as 300.
The situation is that for any given SEMA and LEMA mixture, the LEMA lookback interval must be larger than the corresponding SEMA lookback interval. We’d carry out backtests on all totally different mixtures of those SEMA and LEMA values and select the one which yields the perfect efficiency.
We’ll plot:
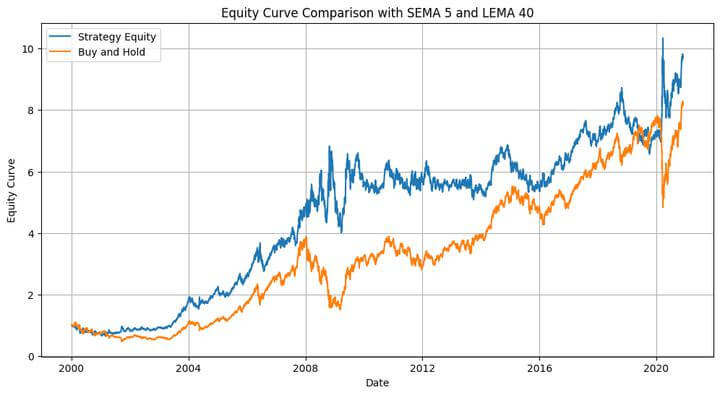
- the fairness curve of the technique with the best-performing SEMA and LEMA lookback values, plotted in opposition to the buy-and-hold fairness,
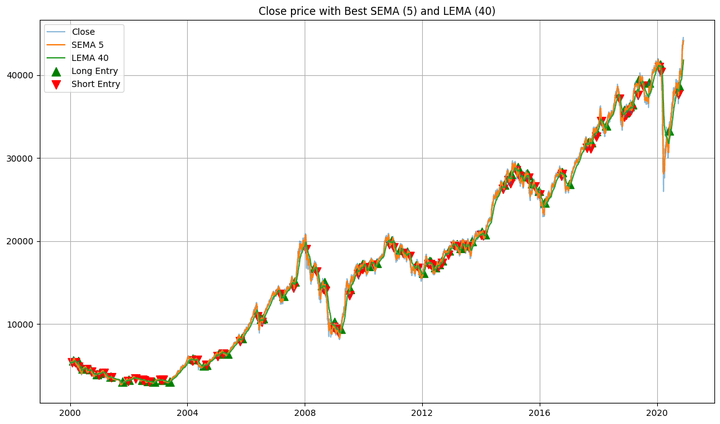
- the purchase and promote alerts plotted together with the shut costs of the in-sample knowledge and the SEMA and LEMA strains,
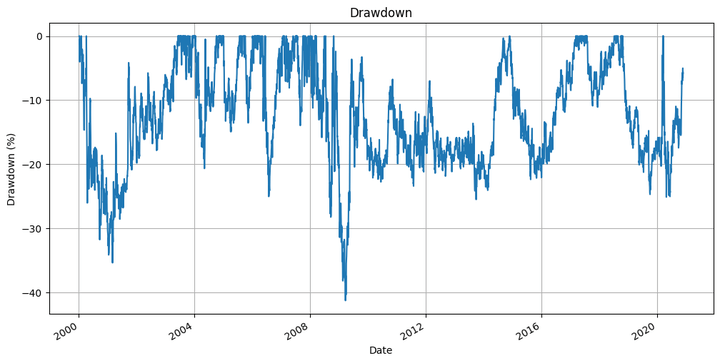
- the underwater plot of the technique, and,
- a heatmap of the returns for various LEMA and SEMA calculations.
We’ll calculate:
- the SEMA and LEMA lookback values for the best-performing mixture,
- the overall returns of the technique,
- the utmost drawdown of the technique, and,
- the Sharpe ratio of the technique.
We can even overview the highest 10 SEMA and LEMA mixtures and their respective performances.
Right here’s the code for all the above:
And listed below are the outputs of the above code:
Greatest SEMA: 5, Greatest LEMA: 40
Complete Return: 873.43% Most Drawdown: -41.28 % Sharpe Ratio: 0.59
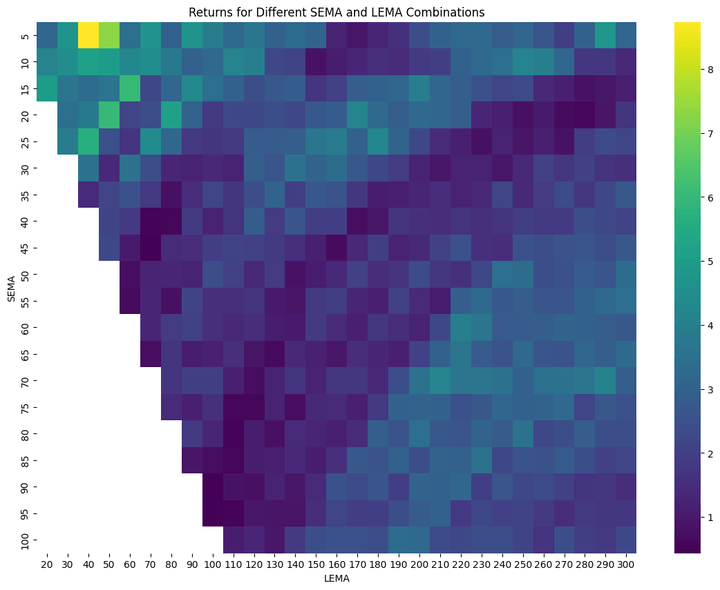
Prime 10 Parameter Mixtures:
SEMA LEMA Return 2 5 40 8.734340 3 5 50 7.301270 62 15 60 6.021219 89 20 50 5.998316 116 25 40 5.665505 31 10 40 5.183363 92 20 80 5.071913 32 10 50 5.022373 58 15 20 4.959147 27 5 290 4.794400
The heatmap exhibits a gradual change in coloration from one adjoining cell to the following. This means that slight modifications to the EMA values don’t result in drastic adjustments within the technique’s efficiency. After all, it might be extra gradual if we have been to scale back the spacing between the SEMA values from 5 to, say, 2, and between the LEMA values from 10 to, say, 3.
The technique outperforms the buy-and-hold technique, as proven within the fairness plot. Excellent news, proper? Notice right here that this was in-sample backtesting. We ran the optimisation on a given dataset, took some info from it, and utilized it to the identical dataset. It’s like utilizing the costs for the following 12 months (that are unknown to us now, besides if you happen to’re time-travelling!) to foretell the costs over the following 12 months. Nonetheless, we are able to utilise the knowledge gathered from this dataset to use it to a different dataset. That’s the place we use the out-of-sample knowledge.
Backtesting on Out-of-Pattern Knowledge
Let’s run the backtest on the out-of-sample dataset:
Earlier than we see the outputs of the above codes, let’s checklist what we’re doing right here.
We’re plotting:
- The fairness curve of the technique plotted alongside that of the buy-and-hold, and,
- The underwater plot of the technique.
We’re calculating:
- Technique returns,
- Purchase-and-hold returns,
- Technique most drawdown,
- Technique Sharpe ratio,
- Purchase-and-hold Sharpe ratio, and,
- Technique hit ratio.
For the Sharpe ratio calculations, we assume a risk-free price of return of 0. Listed here are the outputs:
Out-of-Pattern Technique Complete Return: 15.46% Out-of-Pattern Purchase-and-Maintain Complete Return: 79.41% Out-of-Pattern Technique Most Drawdown: -15.77 % Out-of-Pattern Technique Sharpe Ratio: 0.30 Out-of-Pattern Purchase-and-Maintain Sharpe Ratio: 0.56 Out-of-Pattern Hit Ratio: 53.70%
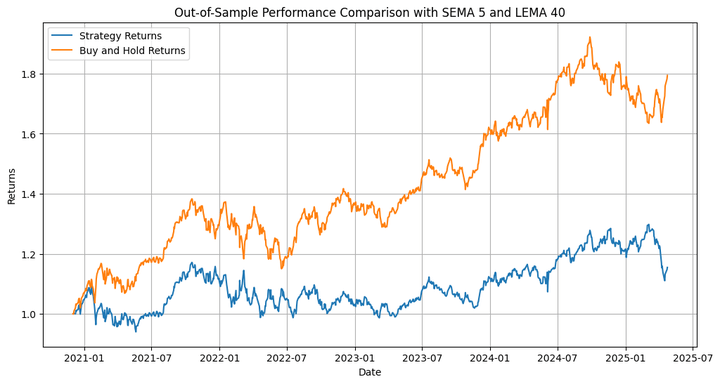
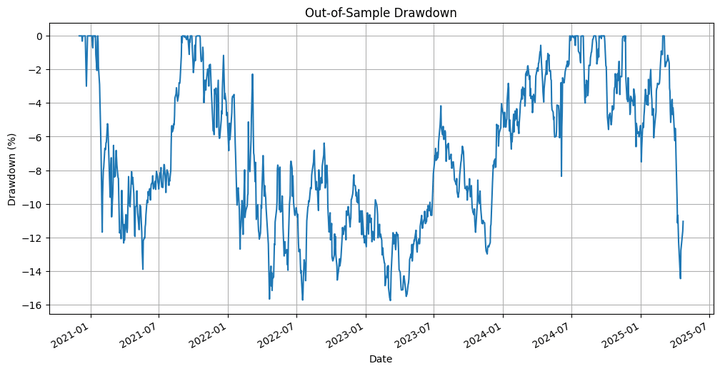
The technique underperforms the underlying by a big margin. However that’s not what we’re primarily fascinated about, so far as this weblog is worried. We have to think about that we ran an optimisation on solely one of many many paths that the costs may have taken in the course of the in-sample interval, after which extrapolated that to the out-of-sample backtest. That is the place we use the simulation we carried out originally. Let’s run the backtest on the totally different simulated paths and verify the outcomes.
Backtesting on Simulated Paths and Optimising to Extract the Greatest Parameters
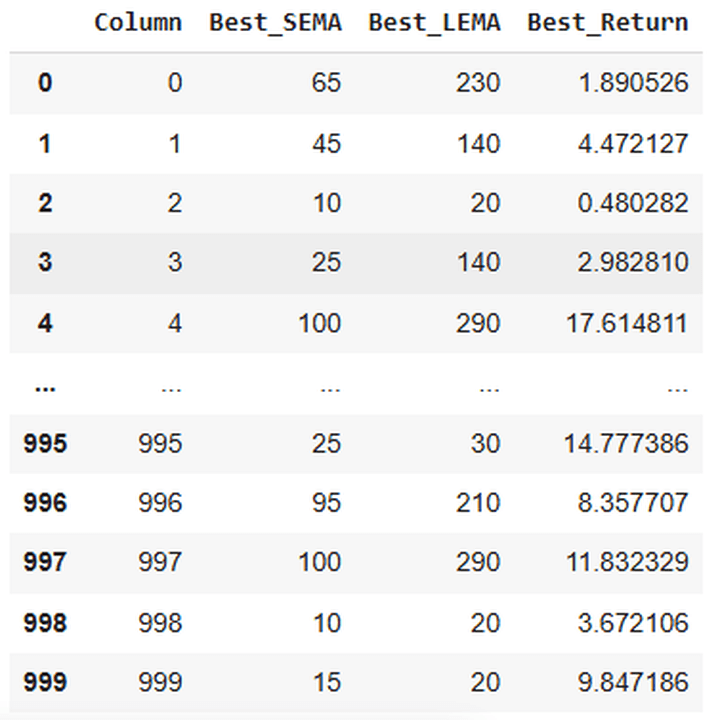
This may hold printing the corresponding SEMA and LEMA values for the perfect technique efficiency, and the efficiency itself for the simulated paths:
Accomplished optimization for column 0: SEMA=65, LEMA=230, Return=1.8905 Accomplished optimization for column 1: SEMA=45, LEMA=140, Return=4.4721 ..................................................................... Accomplished optimization for column 998: SEMA=10, LEMA=20, Return=3.6721 Accomplished optimization for column 999: SEMA=15, LEMA=20, Return=9.8472
Right here’s a snap of the output of this code:
Now, we’ll type the above desk in order that the SEMA and LEMA mixture with the perfect returns for essentially the most paths is on the high, adopted by the second-best mixture, and so forth.
Let’s verify how the desk would look:
Right here’s a snapshot of the output:
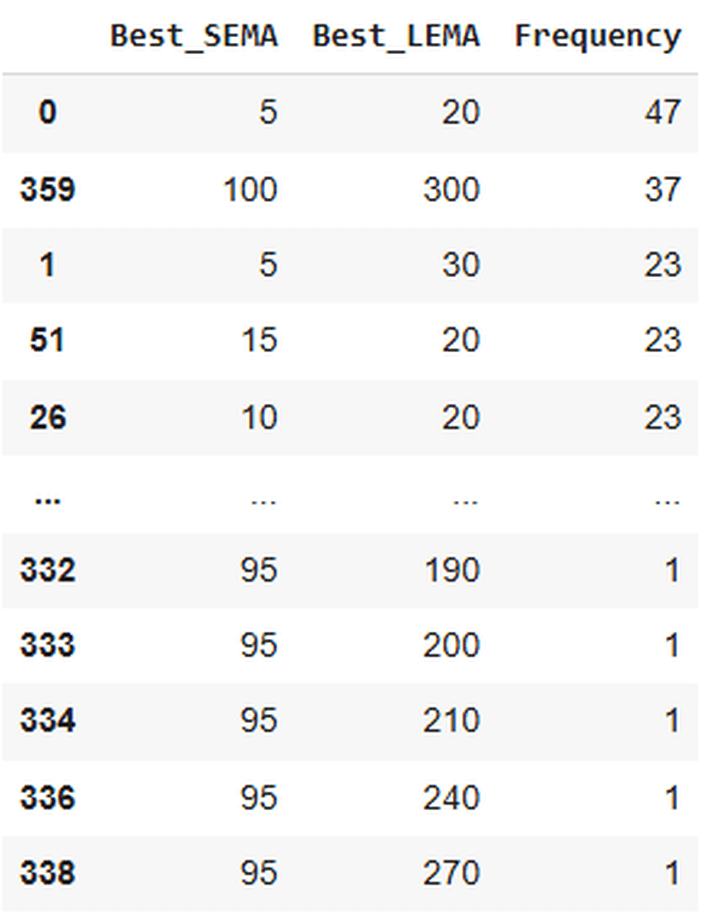
Of the 1000 paths, 47 confirmed the perfect returns with a mix of SEMA 5 and LEMA 20. Since I didn’t use a random seed whereas producing the simulated paths, you may run the code a number of instances and acquire totally different outputs or outcomes. You’ll see that the perfect SEMA and LEMA mixture within the above desk would most definitely be 5 and 20. The frequencies can change, although.
How do I do know?
As a result of I’ve accomplished so, and have gotten the mix of 5 and 20 within the first place each time (adopted by 100 and 300 within the second place). After all, it’s not that there’s a zero likelihood of getting another mixture within the high row.
Out-of-Pattern Backtesting utilizing Optimised Parameters based mostly on Simulated Knowledge Backtesting
We’ll extract the SEMA and LEMA look-back mixture from the earlier step that yields the perfect returns for a lot of the simulated paths. We’ll use a dynamic method to automate this choice. Thus, if as an alternative of 5 and 20, we have been to acquire, say, 90 and 250 because the optimum mixture, the identical can be chosen, and the backtest can be carried out utilizing that.
Let’s use this mixture to run an out-of-sample backtest:
Listed here are the outputs:
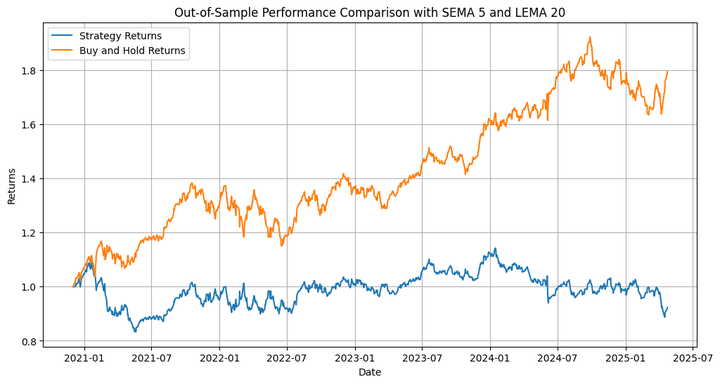
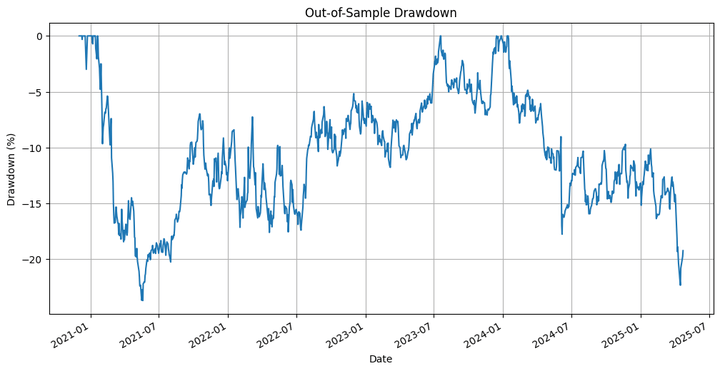
Out-of-Pattern Technique Complete Return: -7.73% Out-of-Pattern Purchase-and-Maintain Complete Return: 79.41% Out-of-Pattern Technique Most Drawdown: -23.70 % Out-of-Pattern Technique Sharpe Ratio: -0.05 Out-of-Pattern Purchase-and-Maintain Sharpe Ratio: 0.56 Out-of-Pattern Hit Ratio: 52.50%
Dialogue on the Outcomes and the Strategy
Right here, the technique not solely underperforms the underlying but additionally generates detrimental returns. So what’s the purpose of all this effort that we put in? Let’s notice that I employed the transferring common crossover technique to illustrate the applying of retrospective simulation utilizing a modified Brownian bridge. This method is extra appropriate for testing advanced methods with a number of circumstances, and machine studying (ML)-based and deep studying (DL)-based methods.
We now have approaches equivalent to walk-forward optimisation and cross-validation to beat the issue of optimising or fine-tuning a technique or mannequin on solely one of many many doable traversable paths.
Nonetheless, this method of retrospective simulation ensures that you just don’t need to depend on just one path however can make use of a number of retrospective paths. Nonetheless, since operating an ML-based technique on these simulated paths can be too computationally intensive for many of our readers who don’t have entry to GPUs or TPUs, I selected to work with a easy technique.
Moreover, if you happen to want to modify the method, I’ve included some recommendations on the finish.
Analysis of VaR and C-VaR
Let’s transfer on to the following half. We’ll utilise the retrospective simulation to calculate the worth in danger and the conditional worth in danger (learn extra: 1, 2, 3).
Output:
Worth at Threat - 90%: -0.014976172535594811 Worth at Threat - 95%: -0.022113806787530325 Worth at Threat - 99% -0.04247765359038646 Anticipated Shortfall - 90%: -0.026779592114352924 Anticipated Shortfall - 95%: -0.035320511964199504 Anticipated Shortfall - 99% -0.058565593363193474
Let’s decipher the above output. We first calculated the day by day % returns of all 1000 simulated paths. Each path has 5,155 days of knowledge, which yielded 5,154 returns per path. When multiplied by 1,000 paths, this resulted in 5,154,000 values of day by day returns. We used all these values and located the bottom ninetieth, ninety fifth, and 99th percentile values, respectively.
From the above output, for instance, we are able to say with 95% certainty that if the long run costs observe paths much like these simulated paths, the utmost drawdown that we are able to face on any given day can be 2.21%. The anticipated drawdown can be 3.53% if that degree will get breached.
Let’s speak in regards to the extremes now. Let’s examine the utmost and minimal day by day returns of the simulated paths and the realised in-sample path.
Realized Lowest Each day Return: -0.1315258002691394 Realized Highest Each day Return: 0.17339334818061447
The utmost values from each approaches are shut, at round 17.4%. Similar for the minimal values, at round -13.2%. This makes a case for utilizing this method in monetary modelling.
Distribution of Simulated Knowledge
Let’s see how the simulated returns are distributed and examine them visually to a traditional distribution. We’ll additionally calculate the skewness and the kurtosis.
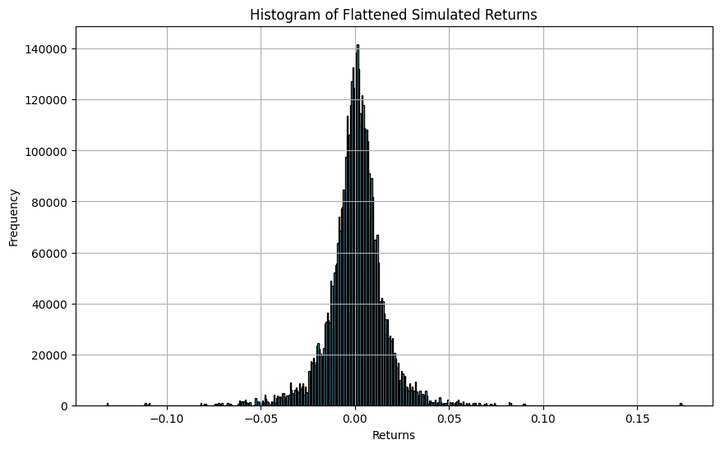
Skewness: -0.11595652411010503 Kurtosis: 9.597364213156881
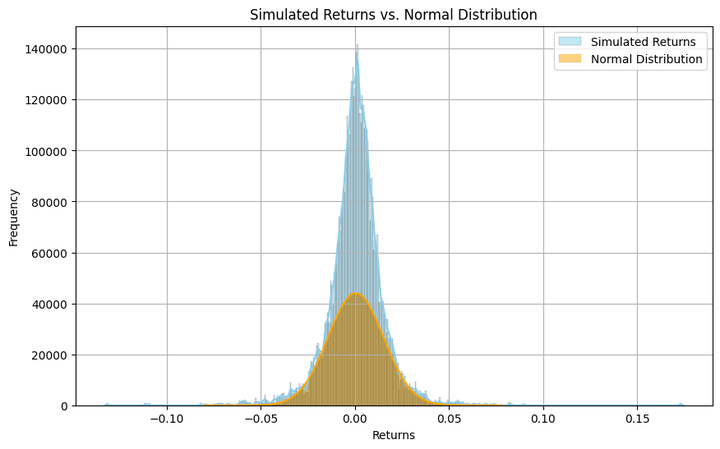
The argument ‘kde’, when set to ‘True’, smooths the histogram curve, as proven within the above plot. Additionally, if you’d like a extra granular (coarse) visible of the distribution, you may enhance (scale back) the worth within the ‘bins’ argument.
Although the histogram resembles a bell curve, it’s removed from a traditional distribution. It reveals heavy kurtosis, that means there are important probabilities of discovering returns which are many commonplace deviations away from the imply. And this isn’t any shock, since that’s how fairness and equity-index returns are inherently.
The place This Strategy Can Be Most Helpful
Whereas the technique I used right here is straightforward and illustrative, this retrospective simulation framework comes into its personal when utilized to extra advanced or nuanced methods. It’s helpful in instances the place:
- You are testing multi-condition or ML-based fashions which may overfit on a single realized path.
- You wish to stress take a look at a technique throughout alternate historic realities—ones that didn’t occur, however very nicely may have.
- Conventional walk-forward or cross-validation strategies don’t appear to be sufficient, and also you need an added lens to consider generalisability.
- You are exploring how a technique would possibly behave (or might need behaved had the worth taken on any alternate value path) below excessive market strikes that aren’t current within the precise historic path.
In essence, this technique allows you to transition from “what occurred” to “what may have occurred,” a delicate but highly effective shift in perspective.
Instructed Subsequent Steps
When you discovered this method fascinating, listed below are just a few methods you may lengthen it:
- Strive extra subtle methods: Apply this retrospective simulation to mean-reversion, volatility breakout, or reinforcement learning-based methods.
- Introduce macro constraints: Anchor the simulations round identified macroeconomic markers or regime adjustments to check how methods behave in such environments.
- Use intermediate anchor factors: As a substitute of simply fixing the beginning and finish costs, attempt anchoring the simulation at quarterly or annual ranges to higher management drift and convergence.
- Prepare ML fashions on simulated paths: When you’re working with supervised studying or deep studying fashions, prepare them on a number of simulated realities as an alternative of 1.
- Portfolio-level testing: Use this framework to judge VaR, CVaR, or stress-test a complete portfolio, not only a single technique.
That is only the start—the way you construct on it is determined by your curiosity, computing assets, and the questions you are attempting to reply.
In Abstract
- The weblog launched a retrospective simulation framework utilizing a non-parametric Brownian bridge method to simulate alternate historic value paths.
- We employed a easy EMA crossover technique to illustrate how this simulation may be built-in into a standard backtesting loop.
- We extracted the finest SEMA and LEMA mixtures after operating backtests on the simulated in-sample paths, after which used these for backtesting on the out-of-sample knowledge.
- This simulation technique allows us to check how methods would behave not solely in response to what occurred, but additionally in response to what may have occurred, serving to us keep away from overfitting and uncover strong alerts.
- The identical simulated paths can be utilized to derive distributional insights, equivalent to tail threat (VaR, CVaR) or return extremes, providing a deeper understanding of the technique’s threat profile.
Regularly Requested Questions
1. Curious why we simulate value paths in any respect?
Actual market knowledge exhibits solely one path the market took, amongst many doable paths. However what if we wish to perceive how our technique would behave throughout many believable realities sooner or later, or would have behaved throughout such realities previously? That’s why we use simulations.
2. What precisely is a Brownian bridge, and why was it used?
A Brownian bridge simulates value actions that begin and finish at particular values, like actual historic costs. This helps guarantee simulated paths are anchored in actuality whereas nonetheless permitting randomness in between. The principle query we ask right here is “What else may have occurred previously?”.
3. What number of simulated paths ought to I generate to make this evaluation significant?
We used 1000 paths. As talked about within the weblog, when the variety of simulated paths will increase, computation time will increase, however our confidence within the outcomes grows too.
4. Is that this solely for easy methods like transferring averages?
In no way. We used the transferring common crossover simply for instance. This framework may be (and must be) used once you’re testing advanced, ML-based, or multi-condition methods which will overfit to historic knowledge.
5. How do I discover the perfect parameter settings (like SEMA/LEMA)?
For every simulated path, we backtested totally different parameter mixtures and recorded the one which gave the best return. By counting which mixtures carried out finest throughout most simulations, we recognized the mix that’s most definitely to carry out nicely. The concept is to not depend on the mix that works on only one path.
6. How do I do know which parameter combo to make use of within the markets?
The concept is to select the combo that almost all often yielded the perfect outcomes throughout many simulated realities. This helps keep away from overfitting to the one historic path and as an alternative focuses on broader adaptability. The precept right here is to not let our evaluation and backtesting be topic to likelihood or randomness, however moderately to have some statistical significance.
7. What occurs after I discover that “finest” parameter mixture?
We run an out-of-sample backtest utilizing that mixture on knowledge the mannequin hasn’t seen. This exams whether or not the technique works exterior of the info on which the mannequin is skilled.
8. What if the technique fails within the out-of-sample take a look at?
That’s okay, and on this instance, it did! The purpose is to not “win” with a primary technique, however to point out how simulation and strong testing reveal weaknesses earlier than actual cash is concerned. After all, once you backtest an precise alpha-generating technique utilizing this method and nonetheless get underperformance within the out-of-sample, it doubtless signifies that the technique isn’t strong, and also you’ll have to make adjustments to the technique.
9. How can I exploit these simulations to know potential losses?
We adopted the method of flattening the returns from all simulated paths into one huge distribution and calculating threat metrics like Worth at Threat (VaR) and Conditional VaR (CVaR). These present how dangerous issues can get, and the way usually.
10. What’s the distinction between VaR and CVaR?
- VaR tells us the worst anticipated loss at a given confidence degree (e.g., “you’ll lose not more than 2.2% on 95% of days”).
- CVaR goes a step additional and says, “When you lose greater than that, right here’s the typical of these worst days.”.
11. What did we study from the VaR/CVaR outcomes on this instance?
We noticed that 99% of days resulted in losses no worse than ~4.25%. However when losses exceeded that threshold, they averaged ~5.86%. That’s a helpful perception into tail threat. These are the uncommon however extreme occasions that may extremely have an effect on our buying and selling accounts if not accounted for.
12. Are the simulated return extremes real looking in comparison with actual markets?
Sure, they matched very intently with the utmost and minimal day by day returns from the true in-sample knowledge. This validates that our simulation isn’t simply random however is grounded in actuality.
13. Do the simulated returns observe a traditional distribution?
Not fairly. The returns confirmed excessive kurtosis (fats tails) and slight detrimental skewness, that means excessive strikes (each up and down) are extra widespread than a traditional distribution would have. This mirrors actual market behaviour.
14. Why does this matter for threat administration?
If our technique assumes regular returns, we’re closely underestimating the likelihood of great losses. Simulated returns reveal the true nature of market threat, serving to us put together for the sudden.
15. Is that this simply a tutorial train, or can I apply this virtually?
This method is extremely helpful in follow, particularly once you’re working with:
- Machine studying fashions which are susceptible to overfitting
- Methods designed for high-risk environments
- Portfolios the place stress testing and tail threat are essential
- Regime-switching or macro-anchored fashions
It helps shift our mindset from “What labored earlier than?” to “What would have labored throughout many alternate market eventualities?”, and that may be one latent supply of alpha.
Conclusion
Hope you discovered a minimum of one new factor from this weblog. In that case, do share what it’s within the feedback part beneath and tell us if you happen to’d prefer to learn or study extra about it. The important thing takeaway from the above dialogue is the significance of performing simulations retrospectively and making use of them to monetary modelling. Apply this method to extra advanced methods and share your experiences and findings within the feedback part. Pleased studying, pleased buying and selling 🙂
Credit
José Carlos Gonzáles Tanaka and Vivek Krishnamoorthy, thanks in your meticulous suggestions; it helped form this text!
Chainika Thakar, thanks for rendering and publishing this, and making it obtainable to the world, that too in your birthday!
Disclaimer: All investments and buying and selling within the inventory market contain threat. Any determination to put trades within the monetary markets, together with buying and selling in inventory or choices or different monetary devices is a private determination that ought to solely be made after thorough analysis, together with a private threat and monetary evaluation and the engagement {of professional} help to the extent you consider mandatory. The buying and selling methods or associated info talked about on this article is for informational functions solely.