Technique, Instance & Python Implementation

By Mohak Pachisia

TL;DR

Most buyers concentrate on selecting shares, however asset allocation, the way you distribute your investments, issues much more. Whereas poor allocation may cause concentrated dangers, a methodical method to allocation would result in a extra balanced portfolio, higher aligned with the portfolio goal.

This weblog explains why Danger Parity is a strong technique. In contrast to equal-weighting or mean-variance optimisation, Danger Parity allocates primarily based on every asset’s threat (volatility), aiming to stability the portfolio in order that no single asset dominates the danger contribution.

A sensible Python implementation exhibits the way to construct and examine an Equal-Weighted Portfolio vs. a Danger Parity Portfolio utilizing the Dow Jones 30 shares.

Key outcomes:

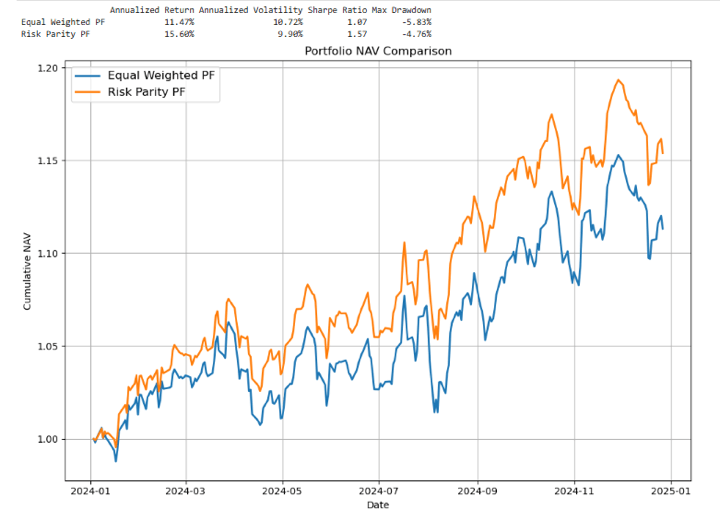
• Danger Parity outperforms with larger annualized return (15.6% vs. 11.5%), decrease volatility (9.9% vs. 10.7%), higher Sharpe ratio (1.57 vs. 1.07), and smaller max drawdown (-4.8% vs. -5.8%).
• Whereas compelling, Danger Parity is determined by historic volatility, it wants frequent rebalancing, and will underperform in sure market circumstances.

To get essentially the most out of this weblog, it’s useful to be aware of a couple of foundational ideas.

Pre-requisites

First, a strong understanding of Python fundamentals is important. This consists of working with fundamental programming constructs in addition to libraries regularly utilized in information evaluation. You possibly can discover these ideas in-depth by means of Fundamentals of Python Programming.

For the reason that weblog builds on monetary information dealing with, you’ll additionally must be snug with inventory market information evaluation. This includes studying the way to acquire market datasets, visualise them successfully, and carry out exploratory evaluation in Python. For this, take a look at Inventory Market Information: Acquiring Information, Visualization & Evaluation in Python.

By masking these conditions, you’ll be well-prepared to dive into the ideas mentioned on this weblog and apply them with confidence.

Desk of contents

Ever questioned the place your portfolio’s threat is coming from?

Most buyers focus closely on choosing the right shares or funds, however what if the method you allocate your capital is extra necessary than the property themselves? Analysis persistently exhibits that asset allocation is the important thing driver of long-term portfolio efficiency. For instance, Vanguard has printed a number of papers reinforcing that asset allocation is the dominant think about portfolio efficiency.

On this put up, we take a more in-depth have a look at Danger Parity, a wise and systematic method to portfolio building that goals to stability threat, not simply capital. As a substitute of letting one asset class dominate your portfolio’s threat, Danger Parity spreads publicity extra evenly, probably resulting in larger stability throughout market cycles.

Quantitative Portfolio Administration is a 3-step course of.

1. Asset choice
2. Asset Allocation
3. Portfolio rebalance and monitoring

In trendy portfolio concept, analysis has proven that “Asset Allocation” has performed a significant position in portfolio efficiency. We’ll perceive Asset Allocation in-depth after which transfer to understanding one of many doable methods to allocate property, the Hierarchical Danger Parity methodology.

What’s Asset Allocation?

Allow us to take an instance of a novice investor. This investor has a portfolio of 5 shares and has invested $30,000 in them.

How he/she purchased particular proportions of the shares may rely on subjective evaluation or on the funds they’ve now to purchase shares. And this results in a random publicity of various shares. As given beneath, let’s assume that the novice investor is shopping for shares, and that is how the allocation appears to be like:

Notice: A few of the numbers beneath might be approximations, for demonstration functions.

In consequence, the proportion of every inventory purchased would broadly range.

Notice: The variety of shares shouldn’t be a complete quantity. The calculations are approximations just for demonstration functions.

We clearly see that NVDA has a considerably larger weightage of 39% whereas APPL has merely a weightage of 6%. There’s a nice disparity within the allocation of funds throughout the totally different shares.

Case 1: NVDA underperforms; it would have a big influence in your portfolio. Which may result in massive drawdowns, and that is excessive idiosyncratic threat.

Case 2: APPL outperforms, as a consequence of a a lot decrease weightage of the inventory in your portfolio. You received’t profit from it.

How Can We Remedy This Allocation Imbalance?

Quantitative Portfolio Managers don’t allocate funds primarily based on subjectivity. It’s business observe to undertake logical, examined, and efficient methods to do it.

Uneven fund allocation can expose your portfolio to concentrated dangers. To handle this, a number of systematic asset allocation methods have been developed. Let’s discover essentially the most notable ones:

1. Equal Weighting:

Method: Assigns equal capital to every asset.

Notice: The variety of shares shouldn’t be a complete quantity. The calculations are approximations just for demonstration functions.

• Execs: Easy, intuitive, and reduces focus threat.
• Cons: Ignores variations in volatility or asset correlation. Might overexpose to riskier property.

Actual world instance: MSCI World Equal Weighted Index

2. Imply-Variance Optimisation (MVO)

Method: Primarily based on Trendy Portfolio Principle, it goals to maximise anticipated return for a given degree of threat. Although it appears to be like easy, this method is adopted by a number of fund managers; its effectiveness comes with periodically rebalancing the portfolio exposures :

1. Anticipated returns
2. Asset volatilities
3. Covariances between property

Notice: The variety of shares shouldn’t be a complete quantity. The calculations are approximations just for demonstration functions.

Monte Carlo simulation is commonly used to check portfolio robustness throughout totally different market eventualities. To know this methodology higher, please learn Portfolio Optimisation Utilizing Monte Carlo Simulation.

The plot beneath exhibits an instance of how portfolios with totally different anticipated returns and volatilities are created utilizing the Monte Carlo Simulation methodology. 1000’s, if no more, combos of weights are thought of on this course of. The portfolio weights with the very best Sharpe ratio (marked as +) are sometimes taken because the portfolio with essentially the most optimum weightages.

Notice: That is just for demonstration functions, not for shares used for our instance.

• Execs: Theoretically optimum: When inputs are correct, MVO can assemble essentially the most environment friendly portfolio on the risk-return frontier.
• Cons: Extremely delicate to enter assumptions, particularly anticipated returns, that are troublesome to forecast.

3. Danger-Primarily based Allocation: Danger Parity

Method: As a substitute of allocating capital equally or primarily based on returns, Danger Parity allocates primarily based on threat contribution from every asset. The aim is for every asset to contribute equally to the full portfolio volatility. The method to realize this consists of the next steps.

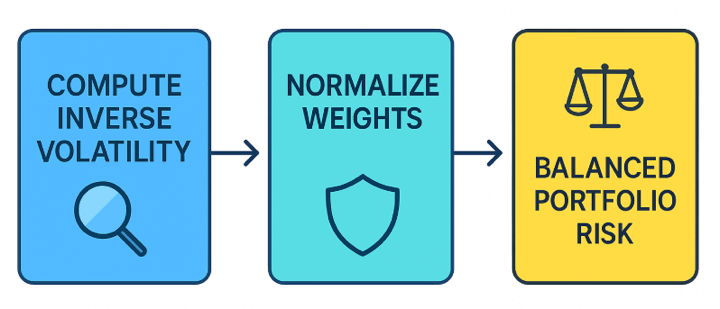
1. Estimate every asset’s volatility
2. Compute the inverse of volatility (i.e., decrease volatility → larger weight).
3. Normalise the inverse of volatility to get closing weights.

What’s volatility?

Volatility refers back to the diploma of variation within the worth of a monetary instrument over time. It represents the velocity and magnitude of worth modifications, and is commonly used as a measure of threat.

In easy phrases, larger volatility means larger worth fluctuations, which may suggest extra threat or extra alternative.

System for Commonplace Deviation:

$$sigma = sqrt{frac{1}{N-1}sum_{i=1}^N (r_i – bar{r})^2}$$

[
begin{aligned}
text{where,}
&bullet sigma = text{Standard deviation}
&bullet r_i = text{Return at time } i
&bullet bar{r} = text{Average return}
&bullet N = text{Number of periods}
end{aligned}
]

Inverse of Volatility:

The inverse of volatility is just the reciprocal of volatility. It’s usually used as a measure of risk-adjusted publicity or to allocate weights inversely proportional to threat in portfolio building.

σ=Volatility

Then the Inverse of Volatility is:  1/σ

Normalise the inverse of volatility to get closing weights :

To find out the ultimate portfolio weights, we take the inverse of every asset’s volatility after which normalise these values in order that their sum equals 1. This ensures property with decrease volatility obtain larger weights whereas sustaining a totally allotted portfolio.

[
w_i = frac{tfrac{1}{sigma_i}}{sum_{j=1}^N tfrac{1}{sigma_j}}
]
$$
textual content{The place,}
bullet w_i quad textual content{= weight of asset $i$ within the portfolio}
bullet sigma_i quad textual content{= volatility (commonplace deviation of returns) of asset $i$}
bullet N quad textual content{= complete variety of property within the portfolio}
bullet sum_{j=1}^N tfrac{1}{sigma_j} quad textual content{= sum of the inverse volatilities of all property}
$$

Instance of Danger Parity weighted method(making use of the above method):

The variety of shares shouldn’t be a complete quantity. The calculations are approximations just for demonstration functions.

Outcome: No single asset dominates the portfolio threat.

Notice:

• Volatility is an instance primarily based on an assumed % commonplace deviation.
• “Danger Parity Weight” is proportional to 1 / volatility, normalised to 100%.
  The publicity is calculated as: Danger Parity Weight × Complete Capital.
• Shares = Publicity ÷ Worth.

Execs:

• Doesn’t depend on anticipated returns.
• Easy, sturdy, and makes use of observable inputs.
• Reduces portfolio drawdowns throughout unstable intervals.

Cons:

• Might obese low-volatility property (e.g., bonds), underweight development property.
• Ignores correlations between property (not like HRP).

Different Allocation Strategies to Know:

Danger Parity Allocations Course of in Python

Step 1: Let’s begin by importing the related libraries

Step 2: We fetch the info for 30 shares utilizing their Yahoo Finance ticker symbols.

• These 30 shares are the present 30 constituents of the Dow Jones Industrial Common Index.
• We fetch the info from one month earlier than 2024 begins. And goal a window of all the yr 2024. That is executed as a result of we use a 20-day rolling interval to compute volatilities and rebalance the portfolios. 20 buying and selling days roughly interprets to at least one month.
• Solely the “Shut” costs are extracted, and the info body is flattened for additional evaluation.

Step 3: We create a operate to compute the returns of portfolios which are both equally weighted or weighted utilizing the Danger Parity method.

Function: To compute a portfolio’s cumulative NAV (Internet Asset Worth) utilizing equal-weighted or risk-parity rebalancing at fastened intervals.

• price_df: DataFrame containing historic worth information of a number of property, listed by date.
• rebalance_period (default = 20):
  Variety of buying and selling days between every portfolio rebalancing.
• methodology (default=”equal”):
  Portfolio weighting methodology – both ‘equal’ for equal weights or ‘risk_parity’ for inverse volatility weights.

Step-by-Step Logic

• Day by day Returns Calculation: The operate begins by computing day by day returns utilizing pct_change() on the value information and dropping the primary NaN row.

• Rolling Volatility Estimation: A rolling commonplace deviation is computed over the rebalance window to estimate asset volatility. To keep away from look-ahead bias, that is shifted by in the future utilizing .shift(1).

• Begin Alignment: The earliest date all rolling volatility is out there is recognized. The returns and volatility DataFrames are trimmed accordingly.

• NAV Initialisation: A brand new Sequence is created to retailer the portfolio NAV, initialised at 1.0 on the primary legitimate date.

• Rebalance Loop: The operate loops by means of the info in home windows of rebalance_period days:

• Volatility and Weights on Rebalance Day: On the primary day of every window:

• Cumulative Returns & NAV Computation: The window’s cumulative returns are calculated and mixed with weights to compute the NAV path.

• NAV Normalisation: The NAV is normalised to match the final worth of the earlier window, making certain clean continuity.

Closing Output: Returns a time sequence of the portfolio’s NAV, excluding any lacking values.

Step 4: Portfolio Development

We now proceed to assemble two portfolios utilizing the historic worth information. This includes calling the portfolio building operate outlined earlier. Particularly, we generate:

1. An Equal-Weighted Portfolio, the place every asset is assigned the identical weight at each rebalancing interval.
2. A Danger Parity Portfolio, the place asset weights are decided primarily based on inverse volatility, aiming to equalise threat contribution throughout all holdings.

Each portfolios are rebalanced periodically primarily based on the required frequency.

Step 5: Portfolio Efficiency Analysis

On this step, we consider the efficiency of the 2 constructed portfolios: Equal-Weighted and Danger Parity, by computing key efficiency metrics:

• Day by day Returns: Calculated from the cumulative NAV sequence to look at day-to-day efficiency fluctuations.
• Annualised Return: Derived utilizing the compound return over all the funding interval, scaled to replicate yearly efficiency.
• Annualised Volatility: Estimated from the usual deviation of day by day returns and scaled by the sq. root of 252 buying and selling days to annualise.
• Sharpe Ratio: A measure of risk-adjusted return, computed because the ratio of annualised return to annualised volatility, assuming a risk-free fee of 0.
• Most Drawdown: The utmost noticed peak-to-trough decline in portfolio worth, indicating the worst-case historic loss.

These metrics supply a complete view of how every portfolio performs when it comes to each return and threat. We additionally visualise the cumulative NAVs of each portfolios to look at their efficiency tendencies over time.

Often Requested Questions

What precisely is Danger Parity?

Danger Parity is a portfolio allocation technique that assigns weights such that every asset contributes equally to the full portfolio volatility, slightly than merely allocating equal capital to every asset. The aim is to stop any single asset or asset class from dominating the portfolio’s general threat publicity.

How does it differ from Equal Weighting or Imply-Variance Optimisation?

• Equal Weighting: This methodology allocates the identical quantity of capital to every asset. It’s easy and intuitive, however doesn’t think about the danger (volatility) of every asset, probably resulting in concentrated threat.
• Imply-Variance Optimisation (MVO): Primarily based on Trendy Portfolio Principle, MVO seeks to maximise anticipated return for a given degree of threat by contemplating anticipated returns and covariances. Nevertheless, it’s extremely delicate to the accuracy of enter forecasts.
• Danger Parity: As a substitute of specializing in returns or allocating equal capital, Danger Parity adjusts weights primarily based on the volatility of every asset, allocating extra capital to lower-volatility property to equalise their threat contributions.

Why is asset allocation so necessary?

Analysis has proven that asset allocation is the first driver of long-term portfolio returns, way more vital than deciding on particular person securities. A well-thought-out allocation helps handle threat and enhances the probability of assembly funding objectives.

How is volatility calculated in Danger Parity?

Volatility is usually measured as the usual deviation of previous returns over a rolling window (for instance, a 20-day rolling commonplace deviation). In Danger Parity, property with decrease volatility are assigned larger weights to stability their contribution to complete portfolio threat.

Is there Python code to implement this?

Sure. The weblog offers full Python code examples utilizing libraries reminiscent of pandas for information dealing with, yfinance for fetching historic costs, and customized capabilities to rebalance portfolios both by equal weights or by inverse volatility (Danger Parity).

Does Danger Parity all the time outperform different methods?

No. Whereas Danger Parity usually results in extra steady efficiency and higher risk-adjusted returns, particularly in diversified or unstable markets, it might underperform easier methods like Equal-Weighted portfolios throughout robust bull markets that favour high-risk property.

What are the constraints of Danger Parity?

• It depends on the historic volatility to set goal weights, which can not precisely replicate  the longer term behaviour of property, particularly throughout abrupt modifications or crises.
• It sometimes requires frequent rebalancing, which may improve transaction prices and potential slippage.
• It might under-allocate to high-growth property in trending markets, limiting upside in robust rallies.

Are there extra superior strategies past commonplace Danger Parity?

Sure. For instance, Hierarchical Danger Parity (HRP) makes use of clustering to grasp asset relationships and goals to allocate threat extra effectively by addressing a number of the weaknesses of conventional mean-variance approaches, reminiscent of instability as a consequence of enter sensitivity.

Conclusion

The comparative evaluation highlights the clear benefits of utilizing a Danger Parity method over a standard Equal-Weighted portfolio. Whereas each portfolios ship constructive returns, Danger Parity stands out with:

• Increased Annualised Return (15.60% vs. 11.47%)
• Decrease Volatility (9.90% vs. 10.72%)
• Superior Danger-Adjusted Efficiency, as seen within the Sharpe Ratio (1.57 vs. 1.07)
• Smaller Max Drawdown (-4.76% vs. -5.83%)

These outcomes show that by aligning portfolio weights with asset threat (slightly than capital), the Danger Parity portfolio might improve return potential together with higher draw back safety and smoother efficiency over time.

The NAV chart additional reinforces this conclusion, exhibiting a extra constant and resilient development trajectory for the Danger Parity technique.

In abstract, for buyers prioritising stability over development, Danger Parity provides a compelling different to standard allocation strategies.

A Notice on Limitations

Though the Danger Parity portfolio delivered stronger returns in the course of the interval taken in our instance, its efficiency benefit shouldn’t be assured in each market part. Like every technique, Danger Parity comes with limitations. It depends closely on historic volatility estimates, which can not all the time precisely replicate future market circumstances, particularly throughout sudden regime shifts or excessive occasions.

It tends to shine in portfolios that blend excessive‑ and low‑volatility property, like shares and bonds, the place equal capital allocation would in any other case focus threat.Nevertheless, if low‑volatility property underperform or if all property have comparable threat profiles,

Moreover, the technique usually requires frequent rebalancing, which may improve transaction prices and introduce slippage. In robust directional markets, notably these favouring higher-risk property, easier methods like Equal-Weighted might outperform as a consequence of their larger publicity to momentum.

Therefore, whereas Danger Parity offers a scientific solution to stability portfolio threat, it must be used with an understanding of its assumptions and sensible limitations.

Subsequent Steps:

After studying this weblog, you could wish to improve your understanding of portfolio design and discover strategies that present extra construction to risk-return trade-offs.

A superb place to start is with Portfolio Variance/Covariance Evaluation, which explains how asset correlations influence portfolio volatility. This may offer you the muse to grasp why diversification works and the place it doesn’t.

From there, Portfolio Optimisation Utilizing Monte Carlo Simulation introduces a extra dynamic method. By operating 1000’s of simulated outcomes, you’ll be able to check how totally different allocations behave below uncertainty and establish combos that stability threat and reward.

To spherical it off, Portfolio Optimisation Strategies walks by means of a spread of optimisation frameworks, masking classical mean-variance fashions in addition to different strategies, so you’ll be able to examine their strengths and apply them in numerous market circumstances.

Working by means of these subsequent steps will equip you with sensible strategies to analyse, simulate, and optimise portfolios, a ability set that’s crucial for anybody seeking to handle capital with confidence.

You possibly can discover all of those intimately within the Portfolio Administration & Place Sizing Studying Monitor, which incorporates the Quantitative Portfolio Administration course for a complete understanding of portfolio building and optimisation.

For these seeking to broaden past portfolio concept into the broader realm of systematic buying and selling, examine the Govt Programme in  Algorithmic Buying and selling – EPAT. Its complete curriculum, led by prime college like Dr. Ernest P. Chan, provides a number one Python algorithmic buying and selling course for profession development. EPAT covers core buying and selling methods that may be tailored and prolonged to Excessive-Frequency Buying and selling. Get personalised assist for specialising in buying and selling methods with stay venture mentorship.

Disclaimer: This weblog put up is for informational and academic functions solely. It doesn’t represent monetary recommendation or a advice to commerce any particular property or make use of any particular technique. All buying and selling and funding actions contain vital threat. All the time conduct your individual thorough analysis, consider your private threat tolerance, and think about searching for recommendation from a professional monetary skilled earlier than making any funding selections.